Хмельник С.И.
Квадратичное программирование
Новый метод и MATLAB-программа
Содержание
-
1. Введение
- 2. Первая задача квадратичного программирования
- 3. Вторая задача квадратичного программирования
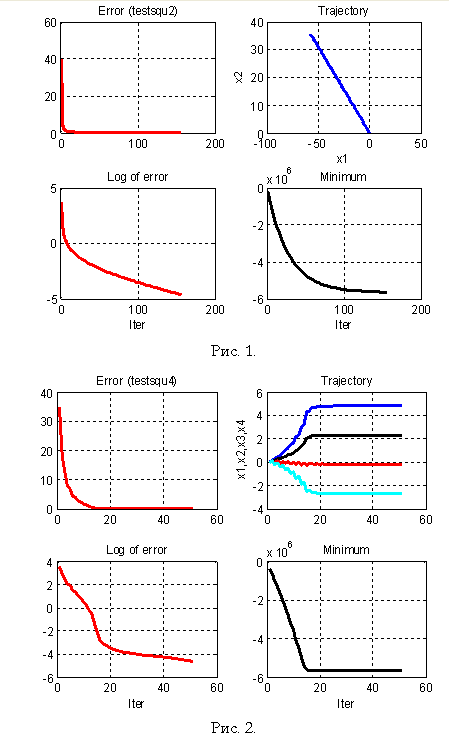
- 4. Тест для первой задачи
- 5. Тест для второй задачи
- 6. Литература
- 7. Программы
- 2. Первая задача квадратичного программирования


Оглавление
-
1. function figi
- 2. function min2_4_300
- 3. function Rdiod
- 4. function squ2
- 5. function squ21
- 6. function testsqu2
- 7. function testsqu4
- 2. function min2_4_300