Содержание
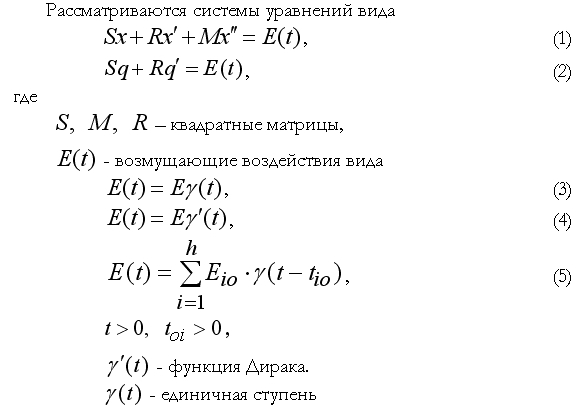

(см. пример 6.3.6 в [1]).
и положительно определенная матрица. При
решение отсутствует. В следующем разделе это ограничение снимается (см. тесты testEDJconv и testEDJconv2).
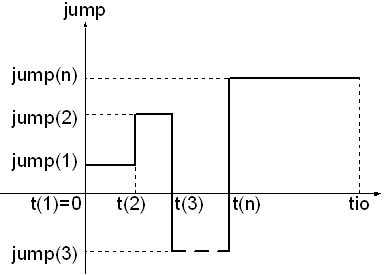
Фиг. 1.
7. Литература
8. Программы
Оглавление
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В книге [1] описан (в частности) новый метод решения указанных задач. В данной книжке описывается программа для такого решения в системе MATLAB. Более полный вариант книжки и открытые коды этой MATLAB-программы можно приобрести у автора на сайте http://mic34.com/bookrumatlab.htm, позиция 357. С предложениями о дополнительных разработках можно обратиться по адресу solik@netvision.net.il. | ||
Содержание
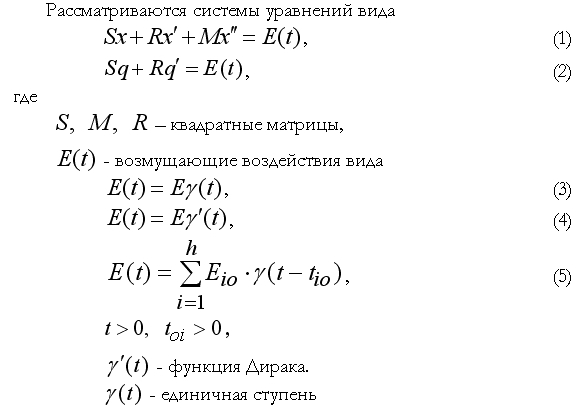


Фиг. 1.
7. Литература
8. Программы
Оглавление
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|