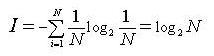 , (3)
, (3)
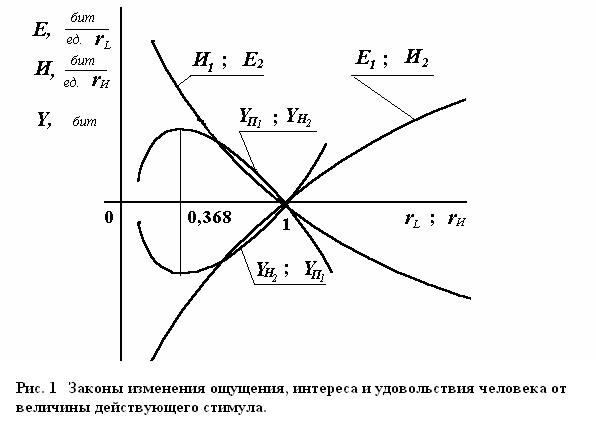
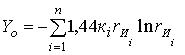 , (8)
, (8)
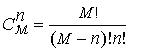 , (9)
, (9)
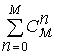 , (10)
, (10)
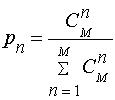 , (11)
, (11)

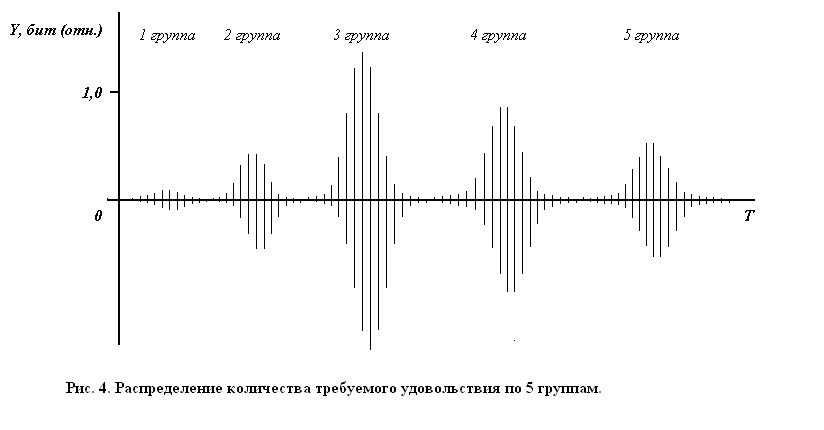
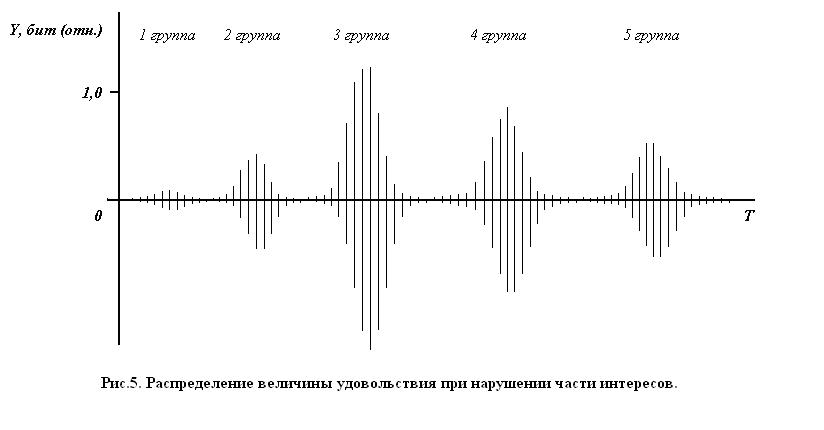
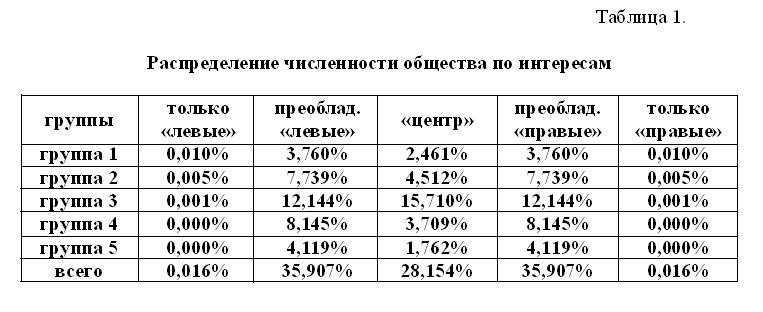
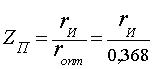 , (15)
, (15)
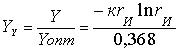 , (16)
, (16)
ЛИТЕРАТУРА
|
|
|
||
М.В. Бахмина, М.А.Кириллов
(Москва)
МОДЕЛИРОВАНИЕ СОЦИАЛЬНЫХ СИСТЕМ НА БАЗЕ
ЗАКОНОВ ПСИХОФИЗИКИ
ПСИХОФИЗИЧЕСКИЕ МОДЕЛИ В СОЦИОЛОГИИ
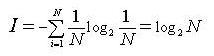 , (3)
, (3)

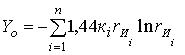 , (8)
, (8)
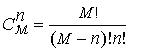 , (9)
, (9)
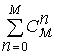 , (10)
, (10)
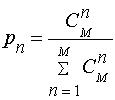 , (11)
, (11)




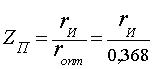 , (15)
, (15)
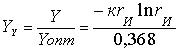 , (16)
, (16)
ЛИТЕРАТУРА
|