Как убежать из-под горизонта черной дыры
Путенихин П.В.
m55@mail.ru
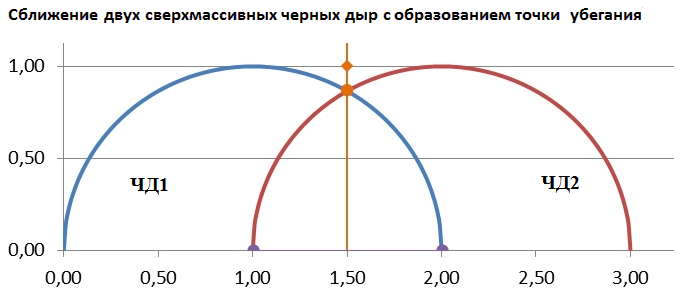
Рис.1 Полуокружности - условное изображение горизонтов двух черных дыр.
![]()
![]()
![]()
![]()
![]()
![]()
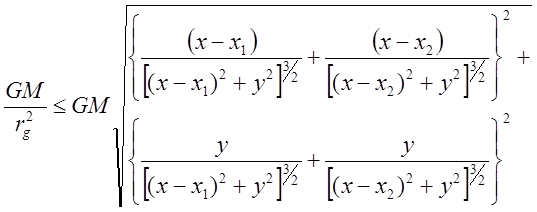
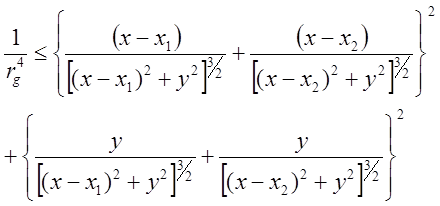
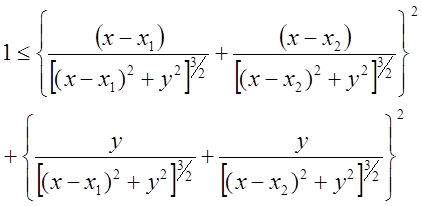
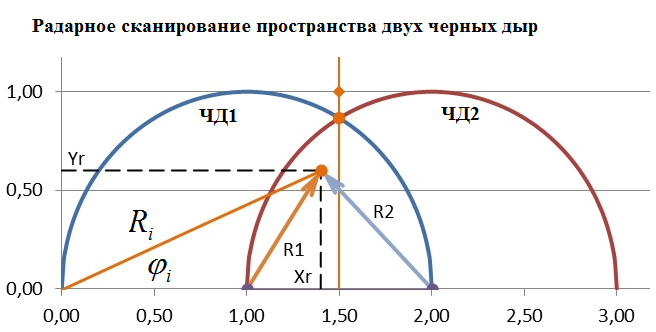
Рис.2 Радарное сканирование пространства вокруг черных дыр для нахождения фантомного горизонта
![]()
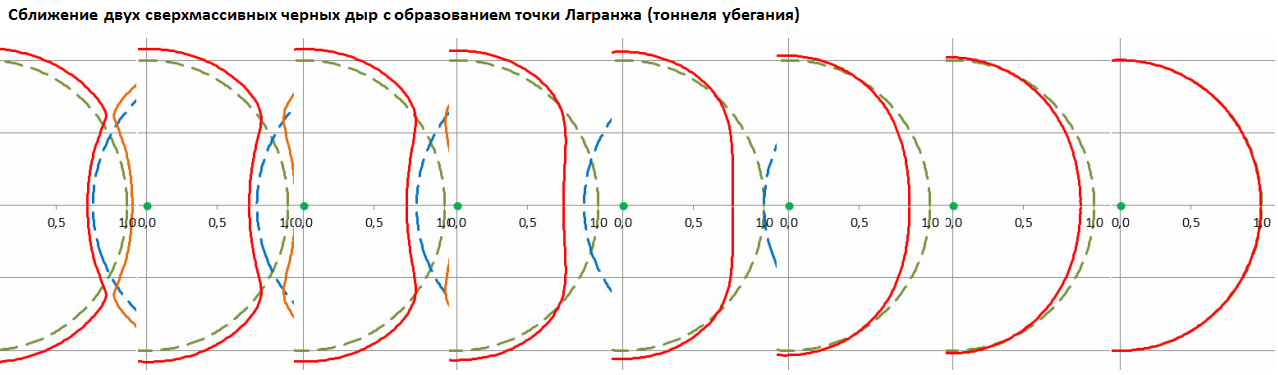
Рис.3 Образование тоннеля фантомного горизонта двух сближающихся черных дыр
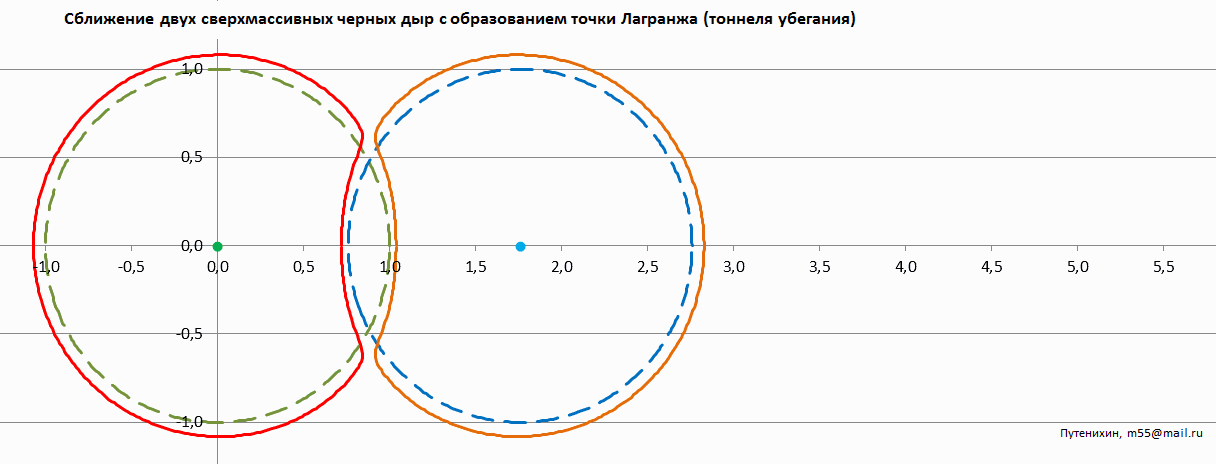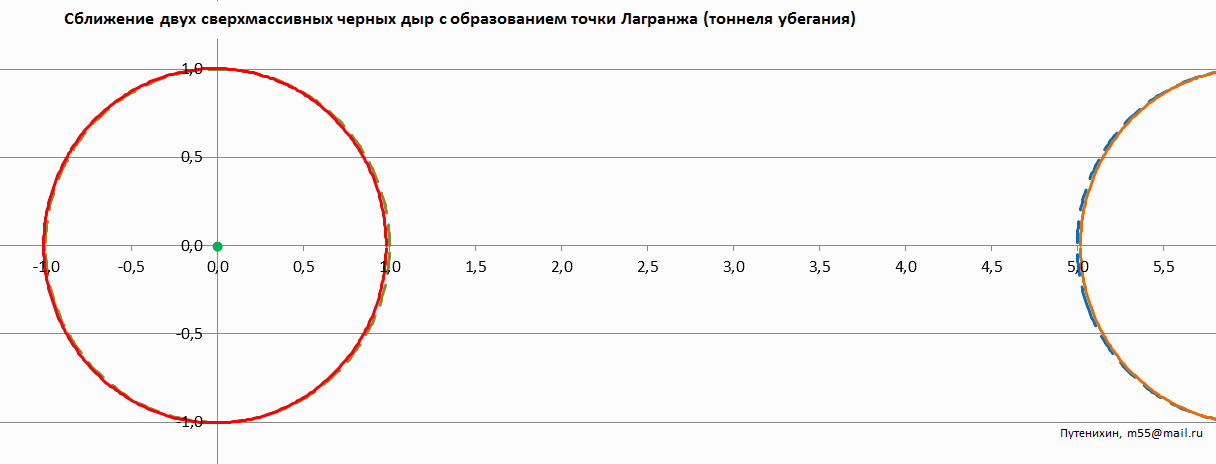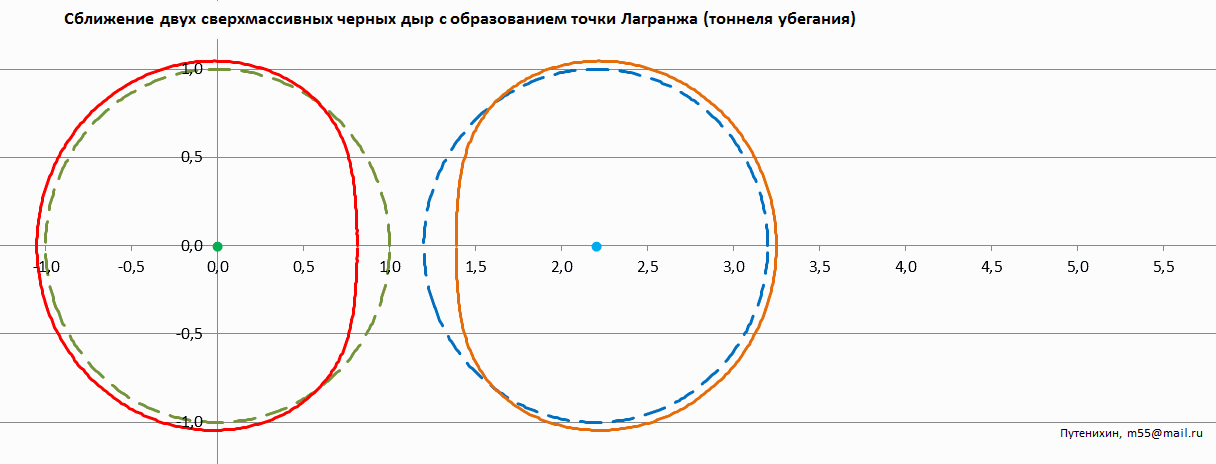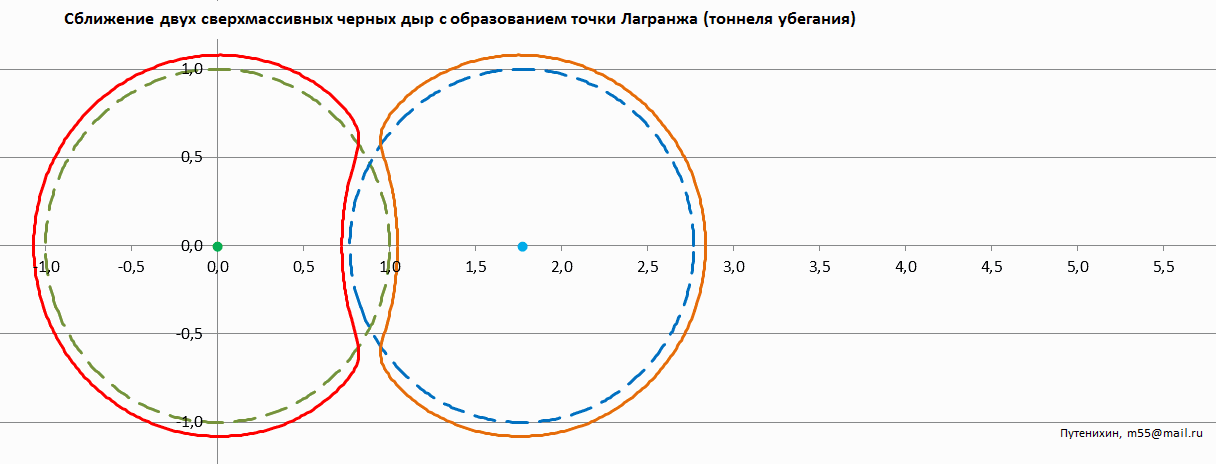
Рис.4 Анимированное изображение сближения двух черных дыр с образованием тоннеля фантомного горизонта
12