Путенихин Петр Васильевич. Парадоксы параллельности. Часть 3. О возможности сравнения векторов

Процедура параллельного переноса векторов чаще всего используется для демонстрации кривизны пространства: перенесённый вектор изменяет своё направление только в искривлённом пространстве. Нередко такая демонстрация представляется в особом свете: утверждается, что обитатель искривлённого мира способен определить его кривизну, не прибегая к понятию пространства погружения. Как мы обнаружили, эта процедура переноса связана с весьма сомнительными выкладками, и фактически является эквивалентным, но довольно усложнённым способом определения кривизны через сумму углов треугольника. Более того, для такого определения кривизны использование параллельного переноса вектора в искривлённом пространстве некорректно, поскольку в искривлённом пространстве параллельных линий нет и быть не может по определению. Некоторые авторы описывают на самом деле эквиугловой перенос, не делая, впрочем, на этом акцента.

Но и в случае использования эквиуглового перемещения, в таких выкладках мы нередко обнаруживаем ряд недомолвок. Главным спорным, вернее даже, ошибочным моментом является то, что в качестве линии переноса зачастую объявляют произвольную линию, линию не являющуюся геодезической. Более замысловатым вариантом является аппроксимация такой произвольной линии бесконечно малыми отрезками геодезических. При этом остаётся незамеченным, что и в этом случае от "геодезической" природы произвольной линии ничего не остаётся.

Бесспорным было и остаётся то, что эквиугловой перенос вектора вдоль геодезической или цепочки геодезических, действительно, приводит к изменению направления вектора, зависимого от выбранного пути. Эти уточнения относительно использования геодезических встречаются нечасто, поэтому повторим: перенос вектора обязательно должен производиться вдоль геодезической или их неразрывной последовательности и с неизменным углом относительно них. При нарушении этих правил переноса закономерно возникают другие, довольно спорные, мягко говоря, трактовки. Пожалуй, наиболее странным и удивительным следует признать утверждение о принципиальной невозможности сравнивания векторов. Буквально это можно трактовать как бессмысленность вообще каких-либо недеформирующих переносов векторов в пространстве.

"Как мы видим в римановой геометрии, в отличие от евклидовой, непосредственное сравнение векторов, удаленных друг от друга, то есть векторов, находящихся в различных точках пространства, невозможно" [21, с.126].

Конечно, можно сказать, что в цитате отвергается процедура всего лишь непосредственного сравнения векторов, однако явно эта непосредственность не описана. Возможно, речь идёт о прикладывании двух векторов друг к другу в конечной точке, при котором они либо совместятся, либо образуют некоторый угол. При этом остаётся неясным, возможно ли такое непосредственное сравнение векторов скоростей двух разных частиц, если они находятся не в удалённых, а в близлежащих точках пространства? Для определённости мы исключаем варианты, когда вектор в процессе перемещения изменяет свою длину, что, строго говоря, возможно, то есть, мы придерживаемся аргументов, отвергающих геометрию Вейля.

Подобную точку зрения о невозможности сравнения векторов, находящихся в разных точках пространства, изложил ещё один автор:

"В отличие от некоторых проблем, с которыми мы столкнулись, у этой проблемы нет решения - мы просто должны научиться жить с тем фактом, что два вектора можно сравнивать естественным образом, только если они являются элементами одного и того же касательного пространства" [3, с.64; 2, c.104].

Является ли указанный в этой цитате естественный образ сравнения тождественным непосредственному сравнению из предыдущей цитаты? Здесь мы видим буквальную трактовку: сравнивать можно только векторы, находящиеся в пространстве Евклида, на плоскости, поскольку касательным пространством обычно считается именно плоскость Евклида. Непосредственно на поверхности сферы таких векторов быть не может вообще. Векторы в касательном пространстве не принадлежат пространству искривлённому, поскольку любые векторы в них могут иметь с "касаемыми" искривлёнными пространствами лишь одну общую точку и ничего более. А точка, понятно, вектором не является, сколько бы касательных пространств мы ни построили.

"Например, две частицы, проходящие мимо друг друга, имеют четко определенную относительную скорость... (которая не может быть больше скорости света). Но две частицы в разных точках изогнутого многообразия не имеют четко определенного понятия относительной скорости - это понятие просто не имеет смысла" [3, с.64; 2, c.104].

Заметим, что фразу "относительную скорость, которая не может быть больше скорости света" саму следует назвать утверждением "относительным". В любой ИСО два фотона могут удаляться друг от друга с относительной удвоенной скоростью света. Расстояние между ними при таком удалении возрастает с удвоенной скоростью света. Согласно кинематике ведущих физических теорий, галилеевой, эйнштейновой, любые скорости - относительные. Правильнее было бы сказать, что смысла не имеют как раз абсолютные скорости, а отношение скоростей указанных частиц мы просто не можем измерить, что, вообще-то, тоже неверно. Отрицание относительной скорости в цитате, по сути, лишает смысла понятие скорости вообще как таковой. В плоском двухмерном пространстве относительная скорость определяется изменением длины наименьшего, геодезического расстояния между объектами за единицу времени, то есть, скоростью изменения длины геодезической, причём не только в плоском, но и в искривлённом пространстве. Очевидно, что никаких физических запретов не имеют ни измерение интервала времени, ни измерение длины геодезической в любой момент времени.

Утверждение об отсутствии, бессмысленности относительной скорости следует признать не просто спорным, оно ошибочно. Соответственно, и утверждение: "не имеют чётко определённого понятия относительной скорости" (курсив в цитате наш) является странным, бездоказательным постулятивным, а вся цитата в целом выглядит как подмена понятий.

Подобные критические взгляды, отметим, довольно редки. Нам встретилось лишь ещё одно, третье высказывание о такой невозможности сравнивания векторов с прямой отсылкой к процедуре их параллельного переноса:

"В общем случае многообразие будет изогнутым, и возникает тонкая проблема, касающаяся того, как сравнивать векторы или более общие тензоры в разных точках на многообразии" [4, с.13].

Оставим без анализа "более общие тензоры", поскольку проблема со сравниванием просто векторов весьма значительна уже сама по себе, хотя и отмечена как "тонкая проблема". Для визуализации этой проблемы, как один из вариантов, в цитате предложено использовать традиционный перенос вектора на поверхности сферы:

"... когда многообразие искривлено, больше не существует однозначного способа сравнения векторов, определенных в разных точках на многообразии. Один из интуитивно понятных способов визуализировать это - рассмотреть перенос геометрического вектора на двумерной сфере, встроенной в трехмерное пространство" [там же].

Общепризнанно, что такой перенос вектора из одной точки в другую на изогнутом многообразии будет зависеть от выбранного пути. Другими словами, в точку назначения в зависимости от выбранной трассы "придут" разные векторы. Следовательно,

"... поскольку нет предпочтительного пути для выбора, мы не можем найти значимый способ сравнения векторов в разных точках на многообразии, то есть в разных касательных пространствах" [4, с.13].

Сразу же возразим: касательные пространства к переносу векторов не имеют никакого отношения, о чём мы неоднократно говорили. Вектора в касательных пространствах не принадлежат в данном случае поверхности сферы. Все векторы на сфере являются отрезками геодезических, то есть, наикратчайших, но кривых линий. Сказанное нами является пока неявным, скрытым опровержением цитаты [4, с.13]. Как мы отметили: вектор - это отрезок, коллинеарный геодезической. То есть, любой вектор на поверхности сферы обязательно сливается с той или иной геодезической. Иначе говоря, этот вектор имеет некое условное направление, задаваемое этой геодезической. Но направление конкретной геодезической на сфере всегда однозначно, предопределено и нигде на ней не меняется. Следовательно, коллинеарный вектор, перемещаемый по этой геодезической, в любой её точке так же всегда имеет одно и то же направление, направление этой геодезической. Подчеркнём: при таком перемещении вектор, как и геодезическая, нигде и никогда не меняет своего геодезического направления. В любой точке сферы, через которую проходит эта геодезическая, вектор в процессе скольжения так же имеет это неизменное направление. Первый вывод, следующий из этих рассуждений как возражение утверждению [4, с.13]: предпочтительный выбор есть, он однозначен и единственно правильный - это геодезическая, соединяющая исходную и конечную точки. Перенос вектора в искривлённом пространстве мы производим не в неопределённость, не в неизвестность, а в однозначно заданную конечную точку, в наш измерительный прибор. Другими словам: линия переноса вектора в любом искривлённом многообразии предопределена. Конечно, можно выбрать между этими двумя предопределёнными точками и какую-либо другую траекторию, любой кривизны и длины. Таких линий на поверхности сферы - бесконечное множество. А геодезическая, проходящая через эти точки, - единственная. Из этого повторно делаем, подтверждаем вывод: предпочтительный путь для выбора есть, и он строго предопределён - это геодезическая, соединяющая исходную и конечную точки. Между двумя точками есть только одна наикратчайшая линия, только одна единственная геодезическая. Мы рассматриваем меридианную систему координат сферы, поэтому все геодезические, проходящие между точками через другую половину сферы, мы отбрасываем.

Однако, могут нам возразить, векторы не всегда лежат вдоль геодезической, соединяющей две точки. На это мы сначала приведём традиционный пример с переносом вектора вдоль экватора и ортогонального ему. Необоснованно, неверно считается, что такой перенос является параллельным. Ошибка в том, что на поверхности сферы в принципе нет параллельных линий, поэтому и никакого параллельного переноса нет и быть не может. Тогда почему вектор при обходе всего экватора в точности совпадает со своим исходным положением? Здесь на самом деле присутствует не параллельный, а эквиугловой перенос вектора. На всём пути своего движения вектор всегда находился под одним и тем же углом к линии переноса, а к экватору - под прямым. И в начале движения и, соответственно, в конце движения. Но прямой угол - это для наглядности демонстрации. Вектор может иметь с линией переноса любой угол. Пройдя полный круг на сфере, причём не обязательно вдоль экватора, вектор вернётся в исходную точку под тем же первоначальным углом, совпав со своим исходным положением. Из этого делаем последний вывод, завершающий наши возражения: перенос вектора вдоль геодезической, соединяющей начальную и конечную точки, всегда сохраняет направление вектора, задаваемого углом к линии переноса, геодезической переноса.

Особо подчеркнём: линия переноса обязательно должна быть единой, неразрывной геодезической. Любое "перескакивание" с геодезической на геодезическую приводит к увеличению расстояния между точками. По определению эквиуглового переноса по неразрывной наикратчайшей, геодезической угол наклона вектора к этой геодезической сохраняется неизменным. Использование для переноса понятий параллельности, касательных пространств и проекций вектора на них только вводит в заблуждение, приводя к ошибочным выводам.

Однако собственно перенос вектора пока ничего нам не сказал о возможности сравнения векторов. Что означает указанная в утверждении [21, с.126] невозможность сравнения векторов? Хорошо, мы перенесли вектор из отдалённой точки в конечную, целевую с соблюдением правил "по геодезической с сохранением угла". Вот они, два вектора, лежат, так сказать, на столе рядом друг с другом. Что дальше? Что мешает нам их сравнить? А мешает, как можно догадаться, отсутствие определения: что такое сравнивание векторов? Действительно, мы можем сравнить длину двух отрезков, веса двух гирь, время происхождения каких-либо событий, но что означает "сравнить векторы"?

Первое, очевидное: мы можем сравнить длины двух векторов. При этом неважно, каким путём они к нам прибыли, поскольку мы постулировали, что при перемещении векторов их модули не меняются. Поскольку вектор - это, по сути, указатель направления, то сравнивать, видимо, и следует эти два разных в общем случае направления. Но как это сделать? Возникает, строго говоря, весьма странная ситуация. На поверхности сферы векторов, имеющих одинаковое направление, не существует вообще. Особенно это заметно с точки зрения пространства погружения. Любой вектор на сфере - это кривая линия. Есть ли у кривой линии направление? Ну, разве что, по кругу. Только как-то странно называть направлением движения постоянно меняющееся... направление. Касательный вектор в данном случае эквивалентом не является.

С точки зрения обитателей сферы, проблема направления выглядит ещё более странно. Например, все без исключения векторы на полюсе сферы имеют одно и то же направление - на смежный полюс. Но они, понятно, друг с другом не сливаются, это разные векторы. Как ни перемещай любой из них на другой полюс, вектор обязательно изменит своё направление - на предыдущий полюс. Выходит, правы цитированные авторы: сравнивать векторы нет никакой возможности? Но в этом случае так же теряет смысл и всякий перенос векторов в искривлённом пространстве. Выходит, что вектор, перемещённый в новую точку, не имеет с исходным вектором ничего общего. Кроме модуля. Иначе говоря, в процессе перемещения вектора он теряет одно из своих определяющих свойств: направленность. Формально он превратился в скаляр, хотя в новой точке у него всё-таки явно есть какое-то направление, новое. Действительно, ситуация выглядит весьма странно. Чтобы разобраться в ней, произведём тестовый перенос на сфере некоторого вектора с соблюдением правила "эквиугловой-геодезическая".

Рассмотрим две точки на поверхности сферы. Пусть одна будет на полюсе, а вторая находится на удалении от неё. Между этими двумя точками и, добавим, между двумя любыми точками, мы можем провести наикратчайшую - геодезическую. В каждой из этих точек строим по вектору. Напомним: каждый из построенных векторов обязательно является отрезком какой-либо геодезической, отрезком большого круга, то есть, отрезком кривой линии. Никакие касательные к сфере пространства, плоскости эти вектора вместить не могут: они будут, так сказать, "выпирать" из этих плоскостей. Но и проекции векторов на эти касательные пространства к нашим векторам имеют крайне отдалённое отношение, имея с ними лишь по одной общей точке. Вопрос, таким образом, состоит в том, как сравнить эти два криволинейных вектора.

Если отбросить различие в их направлениях, то два отрезка больших кругов, векторов в нашем случае, вполне могут иметь одну и ту же скалярную длину. Для определённости постулируем это. Следовательно, вопрос формулируется чуть короче: как сравнить направления этих криволинейных отрезков, отрезков больших кругов? Каждый из векторов, повторим, сливается с той или иной геодезической, большим кругом сферы. Все эти круги, геодезические имеют между собой раз и навсегда заданный угол в точке пересечения. В том числе, углы предопределены попарно так же и между тремя геодезическими: теми, на которых лежат наши вектора, и геодезической, соединяющей их начала, заданные нами точки.

Любой большой круг сферы мы можем вращать вокруг оси, ортогональной к плоскости любого другого большого круга. При этом в точке пересечений этих двух кругов угол будет всегда один и тот же. Это очевидно просто в силу симметрии. Такое вращение можно назвать эквиугловым для вектора, находящегося в точке пересечения геодезических и лежащего на одной из них.

Вращая этим способом один из векторов с его "персональной" геодезической мы обязательно рано или поздно коснёмся их точкой пересечения другой точки. Но эта другая точка - начало второго вектора и теперь уже его "персональной" геодезической. Иначе говоря, оба вектора своими началами, своими начальными точками совместились.

В процессе вращения кругов мы ничего на поверхности сферы не меняли, сохранились все углы между всеми парами участников "вектор-геодезическая", угол между которыми по определению равен нулю, и два угла: "геодезическая между точками" и две "персональные" геодезические.

Далее идёт элементарная арифметика: суммарный угол между векторами однозначно определяется их углами относительно геодезической между точками, линии переноса. Сколько бы мы ни вращали "измеряемый" вектор с его геодезической, при совмещении его со второй, целевой точкой угол между ним и вторым вектором всегда будет определяться этой элементарной арифметикой и всегда будет одним и тем же.

Сначала заметим, что возможный вопрос-возражение: "почему мы вращаем вектор именно вдоль этой геодезической, а не по какой-нибудь другой или по ломаной?" не имеет под собой никаких оснований. Главное: мы используем для переноса вектора наикратчайшую линию, геодезическую, которая на сфере является единственной и наипростейшей.

А теперь решающий вопрос: образовавшийся в результате такого замысловатого вращения угол между двумя векторами, что это за угол? Каков его смысл? Совершенно точно, этот результирующий угол предопределён как исходным углом перемещаемого вектора, так и углом вектора в точке назначения. Поскольку эти два угла, по сути, тождественны соответствующим направлениям векторов, то так и спросим: что означают направления двух совмещённых векторов, разные в общем случае? Очевидно, что возможен и частный случай, когда два вектора в целевой, конечной точке совместятся.

В любом случае некое "привязанное" к поверхности сферы направление переносимого вектора однозначно связано с углом между его перенесённой копией и вектором в конечной точке. Но пока по-прежнему неясно, как именно всё-таки сравнить, количественно, например, в градусах эти два направления, исходные направления двух векторов. Очевидным решением является введение какой-то системы координат, в которой эти направления можно будет охарактеризовать конкретными числами. Но здесь возникает некоторая неопределённость. Использовать декартову, прямолинейную систему координат на искривлённом многообразии, как утверждается [14, с.60], невозможно. Использование же обычной для сферы системы координат в виде меридианов и параллелей также имеет серьёзный недостаток. Любой вектор, описанный в этих координатах, будет иметь разную длину, в зависимости от того в какой точке сферы он находится. Например, на рис.3.1a векторы A и B имеют одинаковую "координатную" длину: два меридиана в ширину и две параллели в высоту. Однако отчётливо видно, что их длины при этом - разные. Одной из причин этого различия является то, что в зависимости от параллели расстояния между меридианными точками различаются. На экваторе интервал между соседними меридианами намного больше, чем вблизи от полюса. Но тогда, может быть, система координат параллель-параллель исправит ситуацию? Между всеми параллелями на поверхности сферы всегда одно и то же геометрическое расстояние. То есть, параллели можно назвать эквидистантными кривыми. Однако нет, этот приём также не приводит к желаемому результату. На том же рис.3.1b видим, что такие же два вектора A и B имеют визуально разную длину, хотя в параллелях каждый из них является диагональю квадрата со сторонами, равными одной параллели.

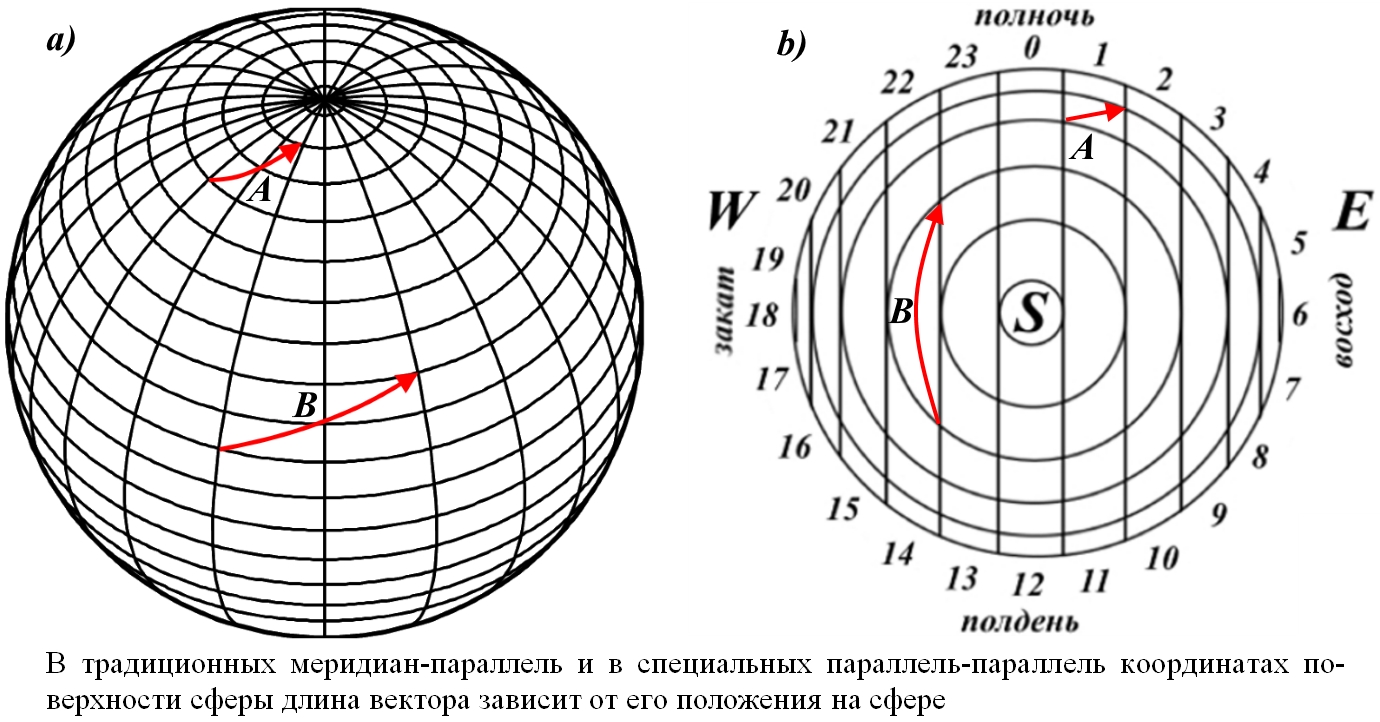
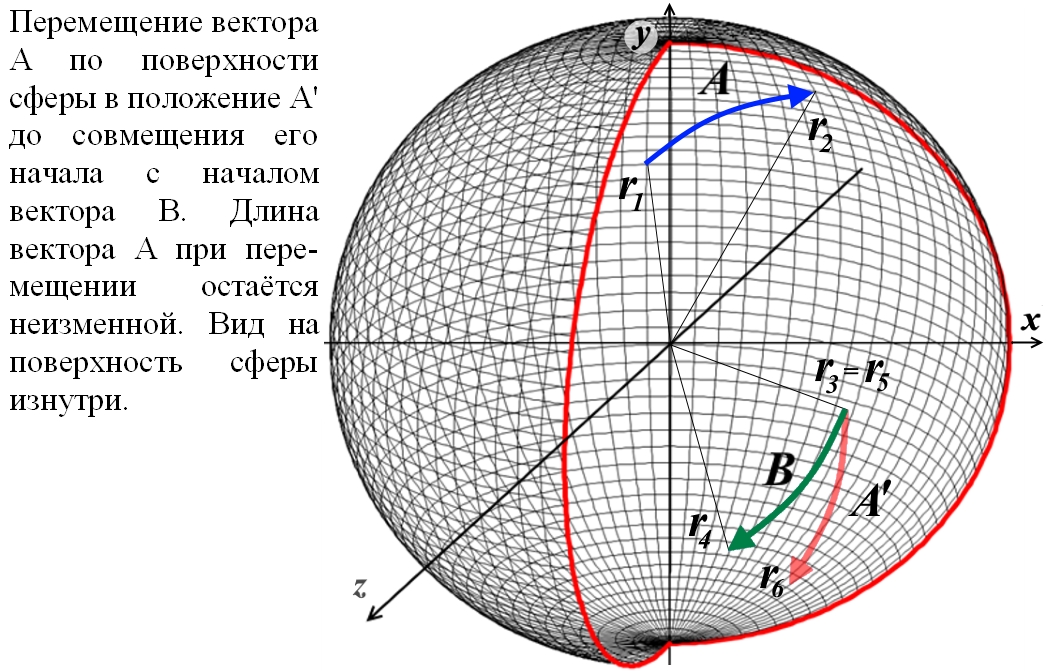
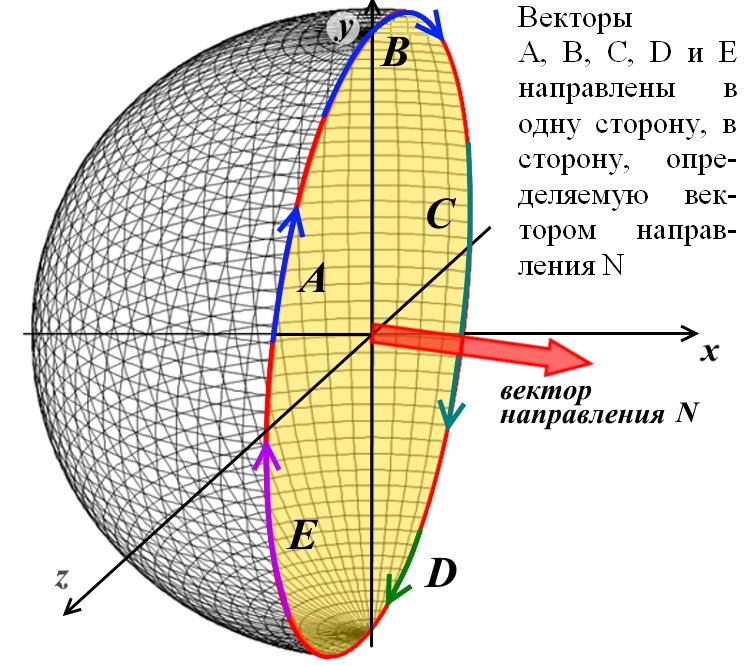
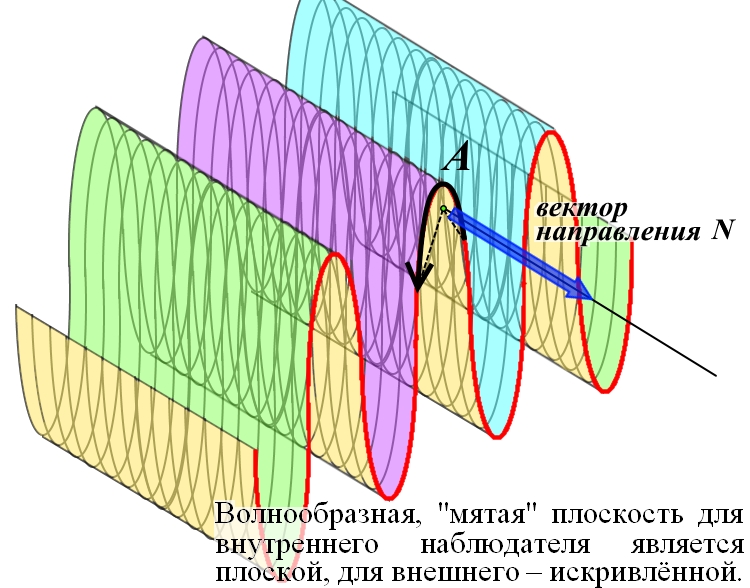
0x01 graphic

Рис.3.1. В традиционных меридиан-параллель и в специальных параллель-параллель координатах поверхности сферы длина вектора зависит от его положения на сфере

И всё-таки проблема имеет решение. Нужно просто использовать сферическую систему координат. Заметим, что эта система описывает трёхмерное пространство, а мы рассматриваем векторы на двухмерной поверхности. Но это не должно быть препятствием, поскольку изначально эту двухмерную поверхность мы рассматриваем именно как находящуюся в пространстве погружения - трёхмерном евклидовом пространстве. Условные обитатели двухмерного мира вполне могут исследовать недоступную им для наблюдения третью координату этой выбранной системы координат. Точно так же, как мы исследуем недоступную для наблюдения в нашем трёхмерном мире четвёртую пространственную координату. Систему координат пространства погружения, разумеется, мы также вольны выбрать из соображений удобства.

Мы будем использовать совместно декартову и частично сферическую системы координат. Координаты всех точек двухмерного многообразия, сферы описываются в декартовой системе уравнением x²+y²+z²= R². Каждый вектор, например, векторы A и B на рис.3.2 мы будем задавать декартовыми координатами их начала и конца. Строго говоря, это не обязательно, но мы считаем это более удобным. Для того чтобы длина вектора была неизменной при его нахождении в любой области сферы, мы задаём правило: векторное произведение радиус-векторов этих двух точек создаваемого вектора должно быть неизменным. Поскольку длины радиус-векторов неизменны и равны радиусу сферы, то неизменным становится и синус угла между ними, то есть, угол. Такое определение, назначение длины вектора можно назвать угловой длиной вектора. На рисунке рис.3.2 приведён пример перемещения вектора A по поверхности сферы до совмещения его начальной точки с начальной точкой другого вектора - B.

Векторы A и B на рисунке образованы радиус-векторами сферы, каждый из которых задаёт точку на её поверхности. Например, вектор A начинается в точке сферы, определяемой радиус-вектором r₁(x₁, y₁, z₁), а заканчивается в точке сферы, определяемой радиус-вектором r₂(x₂, y₂, z₂). При любом перемещении этого вектора по поверхности сферы его длина остаётся неизменной, что обеспечивается неизменностью угла между радиус-векторами r₁ и r₂. Картину перемещения вектора A мы наблюдаем из пространства погружения, причём на рисунке нам видна внутренняя сторона поверхности сферы. Такой вид мы выбрали для того, чтобы были видны радиус-векторы r₁ - r₆. Между началами векторов A и B проводится обязательная единственная геодезическая, Принимаем, что при переносе по ней вектора A угол между ним и этой линией переноса был неизменным, то есть, перенос был эквиугловым.

Очевидно, что перемещение вектора A называть параллельным мы не имеем права - никаких параллелей здесь не просматривается. В качестве линии переноса мы могли бы выбрать произвольную линию, но мы используем правило - переносить только по геодезическим. Такой геодезической на рисунке является большой круг, проходящий через начальные точки векторов - r₁ и r₃. Понятно, что в процессе переноса вектор A мог вращаться вокруг своей начальной точки, но мы вновь придерживаемся правила: угол между вектором A и линией переноса оставляем неизменным и равным его начальному значению. И теперь зададимся вопросом: есть ли какие-либо факторы, способные привести к разным значениям конечного угла между векторами A и B? Более того, сразу же после проведения геодезической между точками r₁ и r₃ нам становятся известны два угла: углы векторов A и B относительно линии переноса, геодезической.

0x01 graphic

Рис.3.2. Перемещение вектора A по поверхности сферы в положение A' до совмещения его начала с началом вектора B. Длина вектора A при перемещении остаётся неизменной. Вид на поверхность сферы изнутри.

Система координат поверхности сферы является сферической, а пространства погружения - декартовой. Между сферическими и декартовыми координатами есть однозначная связь. Это позволяет аналитически определить параметры векторов, необходимые для их перемещения по поверхности сферы. Например, основной, неизменный параметр векторов - их длину - мы установили, предопределили углом между его образующими радиус-векторами. И теперь очень важное замечание: сами эти радиус-векторы позволяют однозначно связать с образованным вектором его направление. Для этого в качестве направления вектора удобно использовать вектор, ортогональный к радиус-векторам рис.3.3. Для выбора из двух возможных, противоположных направлений этого вектора-направления можно использовать традиционное правило буравчика.

Для перемещения мы используем векторы, имеющие одну и ту же длину - угловую длину. Это значит, что все эти векторы имеют векторы направления так же одной и той же длины. Для удобства можно длину вектора направления нормализовать, то есть, принудительно пропорционально изменить декартовы координаты его конца таким образом, чтобы модуль вектора стал равен радиусу сферы. Начало вектора по определению находится в центре сферы.

Таким образом, любой вектор на поверхности сферы имеет однозначно определённое условное направление. Условным направлением мы его называем, потому что геометрически, визуально это направление не является продолжением своего вектора, указывает не туда, не в ту сторону, куда указывает стрелка вектора. Тем не менее, это условное направление изначально является для вектора однозначным, всегда однозначно меняет своё реальное направление при любом перемещении образующего вектора по поверхности сферы и во всех случаях имеет однозначное координатное описание, строго определённые значения координат. Иначе говоря, любой вектор на поверхности сферы имеет длину и направление.

0x01 graphic

Рис.3.3. Векторы A, B, C, D и E направлены в одну сторону, в сторону, определяемую вектором направления N

Бесспорно, выглядит это странно, необычно. Вектор направления N на рис.3.3 ни с одним из "направляемых" векторов A, B, C, D и E не только не имеет общих точек, он к тому же не принадлежит и поверхности сферы, так же не имея с нею общих точек, и не являясь, в том числе, касательным к сфере вектором. Вместе с тем, следует отметить важную особенность этого вектора направления. Все векторы на рис.3.3 визуально направлены в разные стороны. Кажется, что все они указывают в разные стороны. Конечно, это видимость из пространства погружения. Однако рассмотрим положение некоторого вектора на меридиане. Изначально он указывает, скажем, на север. Двигаясь в этом направлении, вектор доходит до северного полюса, по-прежнему указывая на него, на север. Но что произойдёт, когда вектор встанет точно на северный полюс? Если считать, что магнитный полюс точно совпадает с географическим полюсом, то стрелка компаса в этой точке поведёт себя весьма странно: она будет указывать не на север или юг, а точно под ноги, встав строго вертикально. Но наш вектор в этот момент никуда не перемещался и, строго говоря, не менял своего направления. Более того, достаточно переместиться совсем незначительно, и стрелка компаса развернётся на 180 градусов. Стрелка компаса изменила своё направление, а наш вектор - нет. Вектор не изменил своего направления физически, то есть, если в его роли выступает, скажем, реальный, материальный указатель, стрелка на подставке, то этот указатель не вращался. Скажем, в некотором отдалении мы видим какой-то объект, на который направлен указатель. При смещении вектора на незначительное расстояние он по-прежнему будет направлен на этот указатель, но математически, географически теперь указатель-стрелка, вектор сменили своё направления ровно на 180 градусов. Не вращаясь, вектор развернулся на 180 градусов. Теперь он указывает не на север, а на юг. Конечно, всем понятно, что это географическая условность, вращение вектора при переходе через полюс - условность. Однако при движении вдоль экватора никаких подобных условностей не наблюдается. Вектор всегда будет направлен в одну и ту же сторону - на запад или на восток.

Этими двусмысленностью и условностями не обладает вектор направления N на рис.3.3. Всем векторам на рисунке он "назначил" одно и то же направление, которое неизменно при любых смещениях векторов вдоль соответствующей геодезической. При описанных обозначениях координат векторов через их сферические радиус-векторы любая задача о перемещении вектора имеет простое решение: в конкретных числовых обозначениях мы можем сравнивать любые векторы как по их длине, так и по их направлениям. Разумеется, для такого сравнения необходимо установить, задать нулевые, реперные направления, в качестве которых можно использовать, например, те же декартовы координаты пространства погружения.

Разумеется, можно возразить. Во всех предыдущих рассуждениях мы решительно выступали против использования касательных пространств и векторов, поскольку они не принадлежат поверхности сферы, искривлённой поверхности. Тогда почему здесь, в рассматриваемой модели мы используем вектор, который не только не принадлежит искривлённой поверхности, но и с соотносимыми с ним векторами вообще не имеет общих точек. Выглядит как двойные стандарты.

Отчасти это возражение имеет основания. Но сравним связи векторов на поверхности с этими двумя объектами: вектором направления и касательными. Вектор направления всегда связан с интуитивно определяемым направлением вектора. При любом перемещении некоторого вектора по геодезической, его направление считается неизменным, и таким же неизменным остаётся и вектора его направления. Напротив, касательные вектора и касательные плоскости в этой же ситуации ведут себя, мягко говоря, странно. При перемещении вектора каждый раз они указывают на новое направление, куда-то "в небо". Даже на каждое частное направление вектора - на полюс или на запад-восток - эти касательные вектора явно не указывают. Более того, если вектор направления для всех векторов на геодезической один и тот же, то касательные для каждого вектора - собственные и, соответственно, отличаются друг от друга. Таким образом, очевидно, что информативность вектора направления в нашей модели более соответствует ситуации, нежели информативность касательных векторов.

С другой стороны, отсутствие общих точек у вектора на поверхности и вектора направления можно считать относительным. Оба вектора исходят с поверхности большого круга сферы, фактически являясь его производными. Эта общая природа векторов имеет как следствие и жёсткую, нерасторжимую аналитическую связь между ними.

Добавим, что данный формализм определения направлений векторов применим к любым искривлённым пространствам. Рассмотрим, например, волнообразную поверхность на рис.3.4. Вектор направления N заданного вектора A - это вектор, являющийся векторным произведением радиус-векторов r₁(x₁, y₁, z₁) и r₂(x₂, y₂, z₂) начала и конца, формирующих этот заданный вектор. Длина вектора направления N равна произведению длин радиус-векторов r₁ и r₂, умноженному на синус угла между ними. Из этого определения следует очевидный вывод: евклидов вектор, строго прямая линия не имеет сопутствующего вектора направления в выбранной нами сферической системе координат. Действительно, хотя для прямой линии мы можем обозначить длины радиус-векторов его концов бесконечной длины, но в евклидовом пространстве по определению они будут параллельными линиями, то есть, формально в этом случае угол между ними должен быть принят тождественно равным нулю. Отсутствие вектора направления в назначенных координатах следует считать признаком отсутствия кривизны вектора.

0x01 graphic

Рис.3.4. Волнообразная, "мятая" плоскость для внутреннего наблюдателя является плоской, для внешнего - искривлённой.

Однако на рис.3.4 мы видим, что на волнообразной плоскости вектор направления N вектора A в выбранной точке этой плоскости определённо не равен нулю. Возникает двусмысленная ситуация. Для обитателей на волнообразной двухмерной плоскости их мир является строго плоским, евклидовым. Никакими измерениями эти обитатели не смогут определить локальную кривизну своего мира. Сумма углов треугольника всегда будет равна 180 градусам, а параллельный перенос вектора всегда будет сохранять его направление.

С другой стороны: в трёхмерном пространстве погружения мы явно видим, что эта волнообразная, "мятая" поверхность определённо искривлена. Также видно, что на этой двухмерной поверхности прямыми линиями, евклидовыми геодезическими являются только линии, расположенные поперёк волн.

Эти наблюдения высвечивают ещё одну весьма интересную проблему. Считается, что поверхности цилиндра и конуса - плоские, хотя и с некоторыми оговорками. Однако предложенная модель координат и способ построения векторов на этих поверхностях приводят к неожиданному выводу: поскольку существует множество векторов, имеющих ненулевой вектор направления N, эти поверхности конуса и цилиндра являются на самом деле искривлёнными. На цилиндре этот вектор направления максимален вдоль оси цилиндра, а нулевым является только вдоль его радиуса.

Парадокс рецессии

Таким образом, процедура сравнения векторов сводится к двум операциям: a) измерению их длины, модулей и b) измерению их углов относительно геодезической, проходящей через их начальные точки. После этого производится простое сопоставление числовых или геометрических значений этих величин. Утверждение о невозможности такого сравнения, сопоставления является ошибочным. Тем не менее, рассмотренные утверждения о невозможности сравнения векторов получили довольно интересное расширенное толкование:

"В космологии ... очень заманчиво сказать, что галактики "удаляются от нас" со скоростью, определяемой их красным смещением. ... галактики не удаляются, поскольку понятие их скорости по отношению к нам четко не определено" [3, с.64; 2, c.104].

Утверждение, заметим, весьма радикальное, поскольку помимо вопросов перемещения векторов отвергает и фундаментальное положение теории Большого Взрыва. Формально заявлено, что Вселенная не расширяется. Правда, это утверждение входит в некоторое противоречие со следующим в цитате: "не удаляются", но "четко не определено". Нечёткое определение не может служить основанием для радикальной трактовки. Отрицание удаления галактик на основании неопределённости понятия об их скорости относительно нас, наблюдателей, мы считаем ошибочным. Тем более что понятие относительной скорости в описанной ситуации мы считаем строго, чётко определённым.

Следующее далее в цитате пояснение этого расширенного толкования и радикальной трактовки об отсутствии удаления галактик выглядит не менее спорным, чем само толкование.

"На самом деле происходит то, что метрика пространства-времени между нами и галактиками изменилась (Вселенная расширилась) на пути фотона отсюда туда, что привело к увеличению длины волны света" [3, с.65; 2, c.104].

Конечно, наши возражения можно назвать лингвистическим спором. Тем не менее: следует ли отличать, различать, считать разными явлениями увеличение расстояния до галактик вследствие расширения Вселенной, пространства и их удаление от нас. В сущности это одно и то же.

"В качестве примера того, как вы можете ошибиться, наивное применение формулы Доплера к красному смещению галактик подразумевает, что некоторые из них удаляются быстрее света, что явно противоречит теории относительности" [там же].

Что же выходит? Использование эффекта Доплера, наблюдение красных и прочих смещений, космологические измерения скорости удаления галактик, скорости расширения Вселенной, присуждение нобелевской премии за открытие ускоренного расширения Вселенной, поиски тёмных материй и энергий, всё это впустую? Вовсе нет. Ссылка в цитате на теорию относительности в данном случае неверна. Галактики удаляются условно, гипотетически, визуально вследствие расширения пространства, поэтому никакого сверхсветового противоречия нет. Такое удаление галактик, включая якобы и сверхсветовое, как признаётся всеми, а косвенно далее отмечено и в цитате, не считаются реальным, физическим движением. Буквально, галактики удаляются, оставаясь неподвижными. Заметим, что галактики, удаляющиеся быстрее скорости света, не могут наблюдаться в принципе.

"Разрешение этого очевидного парадокса просто в том, что само понятие их рецессии не следует понимать буквально" [там же].

Да, действительно, удаление галактик, рецессию следует понимать с оговоркой, что физическим движением они не являются. В этой связи заметим, что такой подход к "неподвижному удалению" галактик заметно противоречит гипотезе о тёмной энергии, якобы "расталкивающей" галактики. Это расталкивающее усилие определённо означает приведение галактик в реальное, физическое движение, причём с ускорением. При таком подходе сверхсветовое разбегание галактик, противоречащее теории относительности, уже нельзя сбрасывать со счетов.

С другой стороны, трактовке процесса как рецессии, физического разбегания галактик это "неподвижное движение" не противоречит. Длина волны фотона увеличилась не просто так. Фотон движется к нам строго вдоль геодезической, являющейся наикратчайшей линией. Расстояние между галактиками вдоль геодезических увеличилось не мгновенно, а постепенно, что эквивалентно движению их относительно друг друга. Увеличение длины волны полученного нами фотона в точности соответствует скорости нашего "убегания" от него. Согласно трактовке эффекта Доплера, не имеет значения, кто от кого удаляется: источник от приёмника или приёмник от источника. Изменение, увеличение длины волны в этих двух ситуациях одно и то же. Поскольку скорость фотона неизменна, увеличение длины его волны характеризует только скорость разбегания источника и приёмника.

Конечно, по большому счету применение формулы Доплера следует считать всё-таки несколько условным. Можно сказать, что доплеровские измерения определяют не скорость удаления галактик, а увеличение длины геодезической между ними и наблюдателями за время движения фотонов. При этом нет никаких оснований отвергать трактовку такого увеличения длины геодезической как скорости взаимного удаления объектов на её концах. Несмотря на несущественную условность этой трактовки, она даёт хорошие, осмысленные результаты через связь между расстоянием до источника по его яркости и увеличению длины волны.

Кроме того, к галактикам, якобы удаляющимся быстрее света, формула Доплера и не применяется, причём не потому, что физически это движение невозможно. Такие галактики не наблюдаемы, поэтому не существует в принципе и, соответственно, не регистрируется такое красное смещение, при котором скорость могла бы трактоваться как сверхсветовая.

Есть высказывания, что теория Большого Взрыва - плохая теория, но у нас нет ничего лучше (вообще-то, есть [48, с.9]). То же самое, видимо, можно сказать и о красном смещении и доплеровских измерениях. Вероятно, их обоснованность кому-то покажется недостаточной, однако общая картина реальности, созданная с их применением, строго взаимосвязана, непротиворечива внутренне и не противоречит наблюдениям. "Очевидный парадокс" рецессии является иллюзорным. Нет никакого парадокса, определение понятия скорости удаления галактик по отношению к нам является чётким, определённым и в пределах доступной точности - однозначным.

Заключение

Ошибочным является утверждение о принципиальной невозможности сравнивания векторов, что можно буквально трактовать как бессмысленность вообще каких-либо недеформирующих переносов векторов в пространстве.

Утверждение о возникновении ошибок вследствие "наивного" применения формулы Доплера к красному смещению галактик само является ошибочным и наивным.

Ошибочным также является и утверждение о том, что галактики не удаляются от нас. Обоснованием этого "очевидного парадокса" рецессии явилось заявленное отсутствие четкого определения понятие их скорости по отношению к нам. Это заявление ошибочно: никакого парадокса нет. В среде космологов, астрономов определение понятия скорости удаления галактик по отношению к нам является чётким, определённым и в пределах доступной точности - однозначным.

Литература

2. Carroll S. Spacetime and geometry. An Introduction to General Relativity. University of Chicago, Copyright No 2004 Pearson Education, Inc., publishing as Addison Wesley, ISBN 0-8053-8732-3 (hardcover)

3. Carroll S.M. Lecture Notes on General Relativity, arXiv:gr-qc/9712019v1 3 Dec 1997

4. Ekhammar S., Erkensten D., Lassila M., Nilsson T. From Black Holes to Wormholes in Higher Spin Gravity. 2+1-dimensional gravity in a Chern-Simons formulation. Department of Physics, Chalmers University of Technology, Gothenburg, Sweden 2017

14. Бергман П. Загадка гравитации \\Перевод с английского В.А.Угарова. - М.: Наука. Гл. ред. физ.-мат. лит., 1969

21. Вейль Г. Пространство. Время. Материя. Лекции по общей теории относительности: Пер. с нем. Изд. 2-е, испр. - М.: Едиториал УРСС, 2004. - 456 с.

48. Путенихин П.В. Логические основания многомерных пространств. -- Саратов: "АМИРИТ", 2018. - 396 с., цв. илл., ISBN 978-5-907035-29-4, URL: https://www.twirpx.org/file/3089642/
https://www.elibrary.ru/item.asp?id=42690781

23.01 - 29.01.2022

Оставить комментарий © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru) Размещен: 29/01/2022, изменен: 29/01/2022. 45k. Статистика. Статья: Естествознание Геометрия Иллюстрации/приложения: 4 шт. Скачать FB2		Ваша оценка:
Аннотация: Утверждение о принципиальной невозможности сравнения векторов является ошибочным. Определение понятия скорости удаления галактик по отношению к нам является чётким, определённым и в пределах доступной точности - однозначным. The statement about the fundamental impossibility of comparing vectors is erroneous. The definition of the concept of the speed of removal of galaxies in relation to us is clear, definite and, within the limits of available accuracy, unambiguous.

Путенихин Петр Васильевич : другие произведения.

Парадоксы параллельности. Часть 3. О возможности сравнения векторов