THE REALIZABILITY OF THE PENROSE STAIRS
(losses less transitions and results)
Vladimir Utkin u.v@bk.ru
PART 1
(MECHANICS)
INTRODUCTION
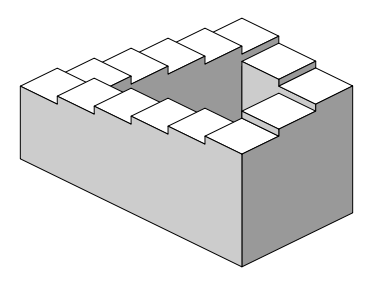
GENERAL APPROACH
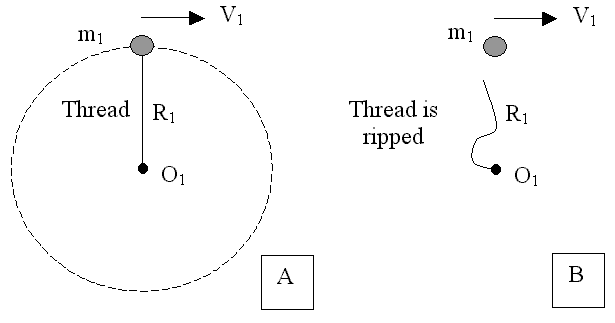
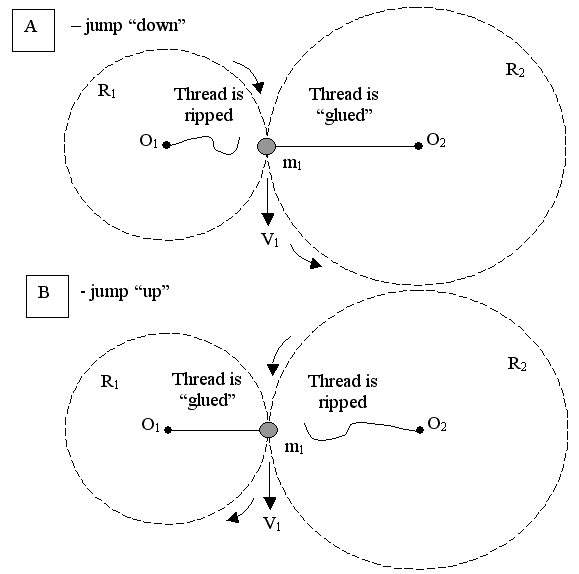
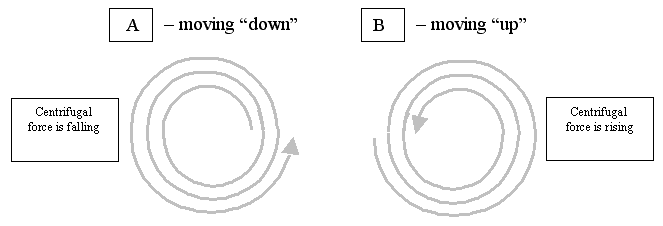
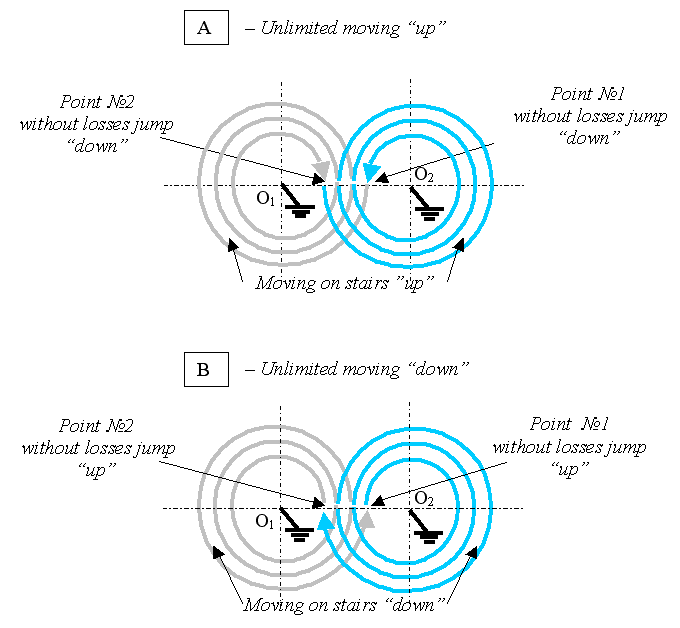
THE POTENTIALLY REALIZABLE VERSION OF THE PENROSE STAIRS
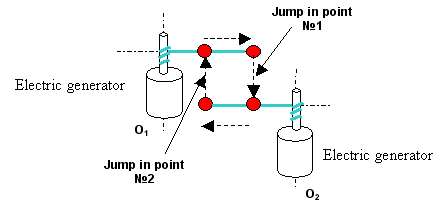
ENERGY GENERATION
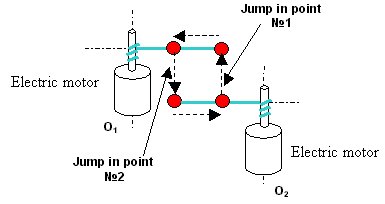
ENERGY DESTRUCTION
THE LAW OF THE CONSERVATION OF THE ENERGY
CONCLUSION
LITERATURE
QUESTIONS AND ANSWERS
(appeared in the process of writing this articles)