Парадокс близнецов - обзор решений, гл.2
Путенихин П.В.
2. Решение парадокса трёх близнецов

Рис.2.1. Сближаются две симметричные ИСО
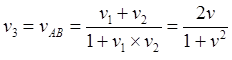
![]()
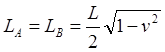 (2.1)
(2.1)
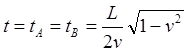 (2.2)
(2.2)
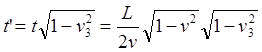 (2.3)
(2.3)
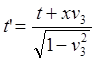
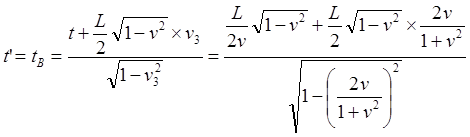
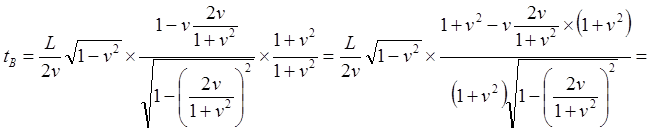
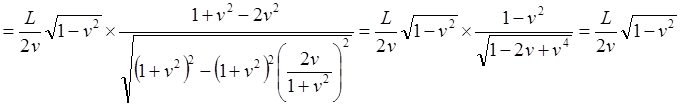 (2.4)
(2.4)
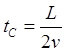
|
|
||
Рассмотрены известные решения релятивистского "парадокса близнецов" и предложены новые. Вопреки распространенному мнению, парадокс имеет корректное решение в СТО. Напротив, в ОТО решения парадокса вызывают ряд вопросов. Рассмотрен принципиально новый парадокс близнецов - в тахионной теории относительности. | ||
Парадокс близнецов - обзор решений, гл.2
Путенихин П.В.
2. Решение парадокса трёх близнецов

Рис.2.1. Сближаются две симметричные ИСО
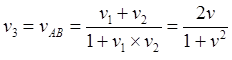
![]()
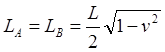 (2.1)
(2.1)
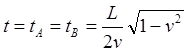 (2.2)
(2.2)
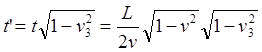 (2.3)
(2.3)
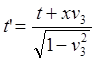
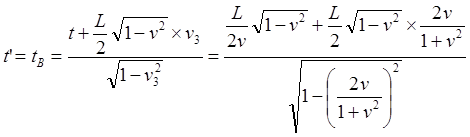
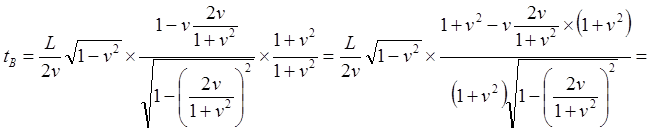
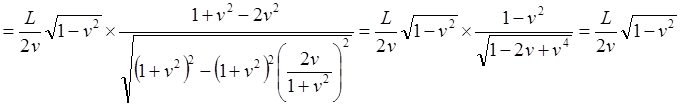 (2.4)
(2.4)
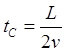
|